The term “vector” refers to the quantity having both direction and magnitude. They are defined using the straight-line, where the length is the magnitude of the Vector, and the orientation indicates what direction the Vector is heading.
Vectors are utilised in math, and there are a variety of vectors, including units vector, collinear vectors, zero vectors, equal vectors, coinitial positive vectors, and many others. Vectors can be used to represent physical objects because they have both magnitudes and directions.
In this article, we’ll understand the definition of Types of Vectors in Maths and much more.
How do I calculate the formula used to calculate vectors?
It is possible to define the Vector -PQ’s magnitude representing the difference between beginning location P and point Q. Additionally, in symbol form, the magnitude of a -PQ can be written as -PQ |. The most important thing is that if the coordinates of the point at which the Vector begins and the ending point of an inverse vector are specified, you can use the formula of distance to calculate the magnitude.
Top 10 Types of Vectors
There are various types of vectors. They are described in the following sections:
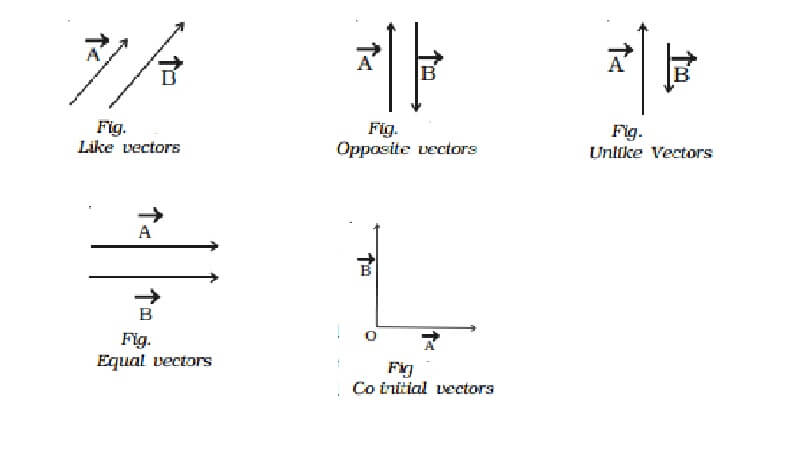
1. Coinitial Vectors
The coinitial vectors are a kind of Vector with two or more distinct vectors that share the same beginning points. In this kind of Vector, each Vector originates from the same location.
The source point will be the same across all vectors and is referred to as coinitial vectors. If, for instance, there are two AB+ and AC- respectively, they are referred to as coinitial vectors because they share a common beginning point called A.
2. Collinear Vectors
The collinear is a different kind of Vector where at least two vectors are in a parallel relationship, regardless of their size or direction. Parallel in nature implies that they don’t cross one another. The direction of both vectors is identical in the natural world. For instance, if vector A is located in x-direction while B is in that same direction, they are referred to as collinear vectors.
Both vectors’ coordinates are identical in the natural world. Another characteristic of a collinear vector is that the cross-product of the two collinear vectors will always be at a value of zero. Another name for collinear vectors is parallel vectors.
3. Zero Vector
A zero vector is a different kind of Vector where the magnitude of the Vector is zero, and the point of origin of the Vector is the point at which it reaches its terminal. For instance, if the Vector is ABis a -> and A’s coordinates and B’s coordinates are the same, then the Vector is referred to as a zero vector.
The direction of the zero Vector is undetermined, and its magnitude remains zero. The zero Vector doesn’t indicate any direction and is also composed of all components equal to zero.
4. Unit Vector
Unit vectors are the kind of Vector with a magnitude equal to the unit length, which is one. Any vector with a magnitude greater than one is called a unit vector. If we consider that there is a vector x-> which has the magnitude x and the unit vector is represented by x, which has the same direction as vector x and magnitude one.
The two vectors can’t be considered equal if they share the same size until each has the same direction.
5. Position Vector
Position vectors are a different kind of Vector where the origin point is regarded as 0, and the source point is an arbitrary point referred to as A within the space. The Vector called OA-> is referred to as the position vector, having the reference origin is 0. It is used to define the location of a point within the 3D dimension Cartesian system. It is determined by reference to any source.
6. Coplanar Vectors
Coplanar vectors are the kind of vectors that have three or more vectors located in the same plane or could be within the same parallel plane. The vectors are called coplanar vectors. There are chances of finding two random vectors within the same plane.
These are referred to as coplanar vectors. The second property of coplanar vectors is that the scalar triple product of three vectors. It is always zero. Coplanar vectors are in a linear dependence.
7. Like and Unlike Vectors
The Like Vectors are the kind of vectors with the same direction and are referred to as like vectors. The vectors with opposite directions, independent of one another, are referred to as Unlike Vectors.
8. Equal Vector
Equal vectors are the kind of vectors in which at least two or three vectors have the same size and identical directions.
9. Displacement Vectors
It is the kind of Vector that occurs when one Vector is moved away from its place; then, it is referred to by its name, displacement vector. For instance, if there’s an object at point A when time 0 and later after some time, it’s located at point B with time = t.
The displacement can be defined by calculating the distance vector between the point at which the object was first positioned and its end-point.
10. Negative Vector
Negative vectors are the kind of vectors where two vectors have an equal amount of power. However, the direction of each Vector is opposite to one other. This kind of Vector is referred to as negative vectors.
Example
In the figure given illustrated below, identify these Vectors: Collinear, Equal and Coinitial.
Here’s the Solution: By definition, we know:
- Collinear vectors are when two or more vectors run parallel to the same line no matter their magnitudes and direction. Hence, in the given figure, the vectors prove to be collinear: a⃗ , c⃗ , and d⃗ .
- Regardless of their initial points, Equal vectors have the same direction and magnitudes. Hence, in the figure above, the a⃗ and c vectors are equal.
- Coinitial vectors mean that two or more vectors have the same initial point. So, in the figure above, the b⃗ , c⃗ , and d⃗ vectors are coinitial.
Conclusion
The vectors are mathematical concepts. There are multiple vectors like coplanar vectors, like and unlike vectors, collinear vectors, unit vectors, displacement vectors, and many more defined above. Don’t get confused while understanding these! The vectors can be described as the physical quantity having direction and magnitude.